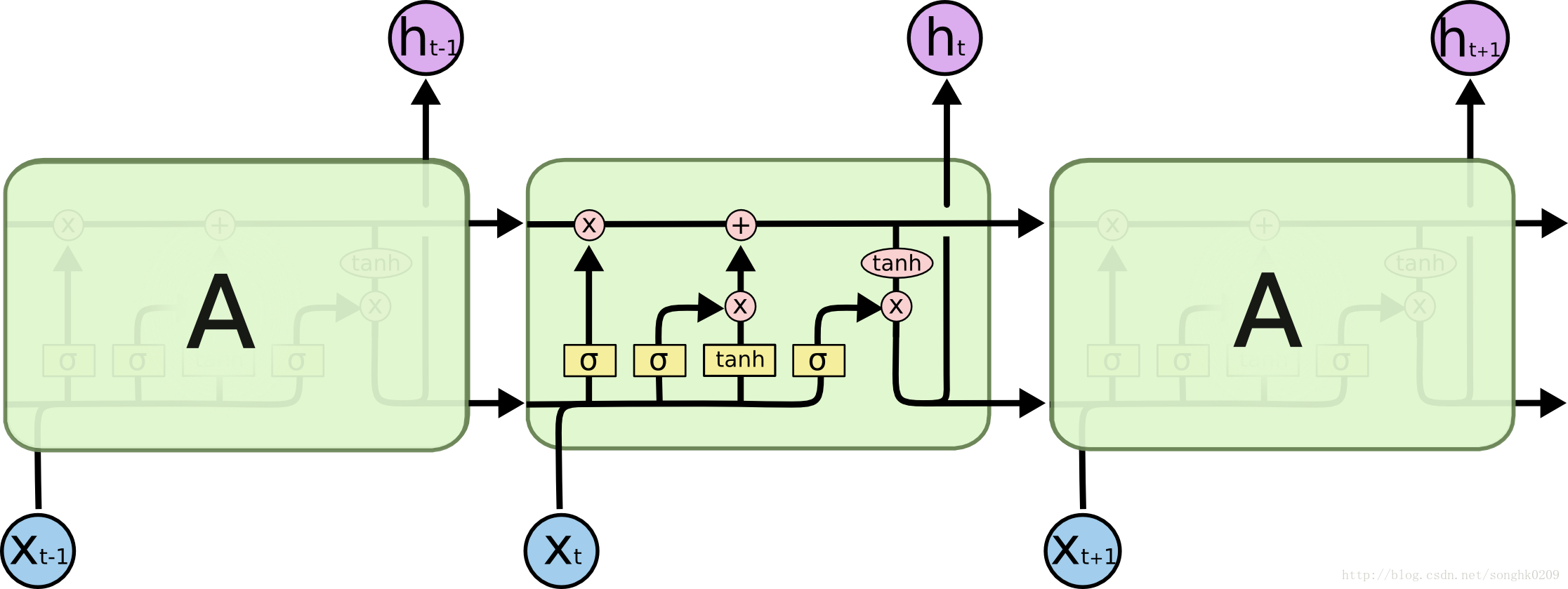
LSTM - 你还记得吗?该忘的就忘了吧。
一时兴起,来推导一下 LSTM(Long Short Term Memory - 长短期记忆)…… 在处理序列型数据时,我们常常使用循环神经网络(RNN),这正是 LSTM 的前身。
一时兴起,来推导一下 LSTM(Long Short Term Memory - 长短期记忆)……
LSTM 从何而来?
在处理序列型数据时,我们常常使用循环神经网络(RNN),这正是 LSTM 的前身。
最简单的 RNN
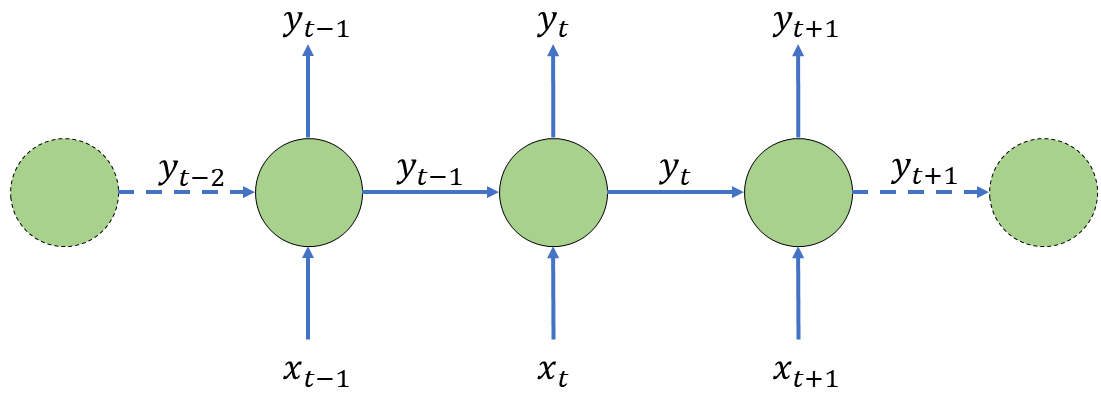
我们先从最简单的无隐层 RNN 开始。它的状态更新方程满足(\(f\) 是某激活函数):$$\hat y_t = f(x_t*W+\hat y_{t-1}*V+b)$$
通过这种方式,每个神经元都会在计算 \(t\) 时刻输出时考虑上一个神经元得出的 \(\hat y_{t-1}\)。也就是说,在每次做决策时,该神经元都会受到上一个决策结果的影响,通过 \(t-1\) 与 \(t\) 的关系,我们也就对整个序列中的元素建立了联系。
然而事实并非如此,想想人类的在考虑序列式问题时的思维模式,假设你正在打麻将牌,对于一般的人而言,每个时刻(出牌时)都会:
- 看看摸到了什么牌,手牌又如何。
- 回顾之前的牌局。
- 通过 1 和 2 分析出当前的最优策略。
第 1 步中的摸牌和看手牌视为当前时刻的输入数据 \(x_{t}\)。第 2 步中的回顾牌局就是访问记忆。而第 3 步就是通过这些信息做出决策求 \(\hat y_t\)。但是不难发现,我们访问的记忆信息不只是上一步做出的决策 \(\hat y_{t-1}\),而是对整个牌局的回顾,即使记忆模糊却也包含了许多信息,至少,它应该是根据最近几个回合的牌局产生的抽象记忆。
携带隐层节点的经典 RNN
所谓的抽象记忆,其实就是 RNN 中的隐状态。我们可以把 \(t\) 时刻神经元的输出看作是两部分,一部分是决策 \(\hat y_t\),另一部分就是隐状态 \(h_t\)。传递给 \(t\) 时刻的信息不再是简单的决策 \(\hat y_{t-1}\) 而已,而是历史记忆的融合 \(h_{t-1}\)。
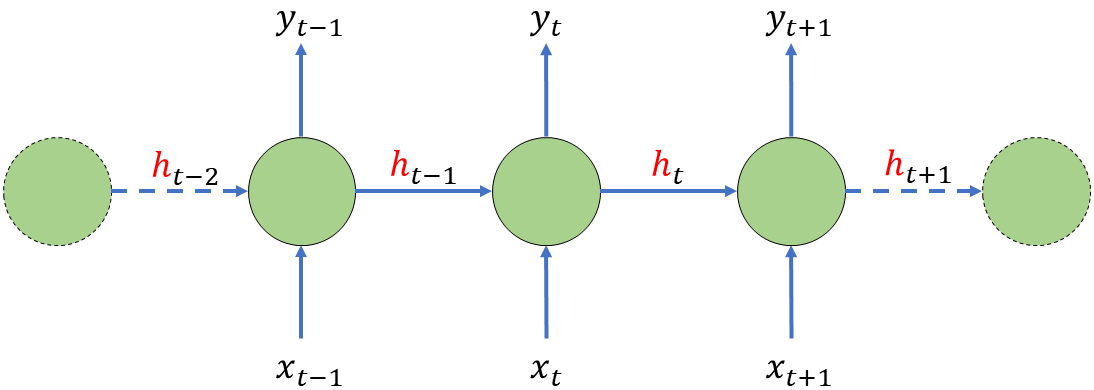
如上图所示,这就是经典 RNN,它的状态更新满足方程(\(f,g\) 均为激活函数):
$$ \begin{align} h_t&=g(x_{t}*U+h_{t-1}*W+b)
\\ \hat y_{t}&=f(h_{t}*V+c) \end{align}$$
这样一来,过去某一个 \(\hat y_{i}\) 可能会通过影响 \(h\) 来影响 \(y_{t}\)。
传统 RNN 的弊端
从上面的 RNN 状态更新方程不难发现,作为“历史记忆”的 \(h\) 其实是套在 \(g(\cdot)\)这个函数里的,也就是说,在误差逆传播的时候,由于求导链式法则,梯度会被表示成连积的形式,当 RNN 的长度 \(\tau\) 较长的时候,梯度从第 \(\tau\) 个神经元传至第一个时,终会弥散或是爆炸(不等于 1 的数连乘)。
这会导致什么呢?在某个时刻出现的重要事件由于时间相隔长远,可能无法对记忆造成影响。依然举麻将的例子。某一刻你摸到了一张牌,你发现可以留着这张牌用来听牌,却忘记了你要听的那张牌很久以前的回合中就已经被打完了——长远记忆丢失了。
(虽然可以用梯度截断的 trick,但还是会丢失部分长远的记忆,这里不作详细介绍)
解决梯度弥散/爆炸问题
在传统 RNN 里,梯度信息经过若干时刻后会弥散或爆炸,我们怎样才能将梯度毫无损失地传输给各个神经元呢?
从之前的讨论可以提出问题:什么梯度在经历了连续的乘积作用后依然能够有效传输呢?当然是 1 啦!也就是说,记长时记忆单元为 \(c\),那么我们要求 \(c_t = c_{t-1}\),即 \(\nabla c_t = 1\)。
这样就不存在什么弥散 or 爆炸的问题了,\(c\) 以某种方式包含着我们需要的信息,能把梯度反馈若干层也不会有任何损失。
长时记忆单元中的信息如何保存
其实上面说的“某种方式”才是重点,我们在最简 RNN 的基础上讨论一下这个问题。那么这个时候我们的新信息就是 \(t\) 时刻的输入 \(x_t\) 与上一时刻的输出 \(\hat y_{t-1}\) 组合后的结果,记作 \(\hat c_t\)。$$ \hat c_t = f(x_t * W, \hat y_{t-1} * V) $$
现在要做的事情是,把 \(\hat c\) 放进 \(c\) 里。由于链式求导法则,我们肯定摒弃乘法操作。
乘法操作更多的是作为一种对信息进行某种控制的操作(比如任意数与 0 相乘后直接消失,相当于关闭操作;任意数与大于 1 的数相乘后会被放大规模等),主要用于控制或者 scaling。
加法操作则是新信息叠加旧信息的操作。
我们选择用加法操作,那么此时有:$$c_t=c_{t-1}+\hat c_{t}$$
然而,每次有新信息时,我们并不是选择将所有的 \(\hat c_t\) 都添加进 \(c_t\) 里,这也和人类记忆方式是相违背的,我们没有必要将每一时刻的所有信息都放进大脑里,我们只记忆那些我们关注的东西。
如何控制记还是不记?首选乘法操作,我们在 \(\hat c_t\) 前加入一个控制器,决定我们要不要记忆新信息。那么对于单个长时记忆单元,我们有:$$c_t=c_{t-1}+g_{in} * \hat c_t$$
我们称其中的 \(g_{in}\) 为输入门,它需要在 \( [0,1]\) 上取值,通常选用 \(sigmoid(\cdot) \) 函数。
此时我们的简单网络就变成了:$$\begin{align} c_t &= c_{t-1} + g_{in}( \hat c_t) \\ \hat c_{t} &= f(x_t * W + \hat y_{t-1} * V) \\ \hat y_{t} &= f(c_{t}) \end{align}$$
现在输入门会学习该在什么时候开启以读入信息并存入记忆。
信息量巨大时会发生什么?
如果仅仅停留在当前这种架构,一定会发生某些问题,比如,当你的网络读到一段信息量巨大的文本时,输入门大开,试图记录所有的信息,也就是说,\(\hat c\) 会变得非常大。
那么问题来了,输入门我们选择的是 \(sigmoid(\cdot)\),很显然当自变量过大时,该函数几乎完全饱和了(趋近于1),根本记不住那么多东西了。
(正向无饱和的激活函数如 ReLU 可以解决这个问题,但是会导致更多的问题)
寻找解决方法时,依然往人类身上想。我们可以记得一年前一场麻将输了一千块(拒绝赌博),也记得一天前的麻将赢了20块,大脑并没有一直只是在记东西——我们并没有顺带着记住这之间的其他所有事情,我们还忘记了一些其他的事情(比如几个月前的晚上和舍友斗地主输了一包辣条)。人的大脑是会忘事的。
我们再用一个控制门吧,用一个“遗忘门”来决定要不要忘记之前的一些不太重要的记忆,以记住新信息。
与输入门的设计思路相似,我们给上一时刻的信息添加一个控制遗忘程度的门 \(g_{forget}\),即:$$c_t = g_{forget}(c_{t-1}) + g_{in}(\hat c_{t})$$
那么现在我们的网络就能解决新旧信息的合理记忆与遗忘问题了,这一点上已经与人类相似。
输出似乎还要再筛选一下
疯狂举例ing:你在打牌时,并不会参考上周六晚吃烧烤摊时拉了肚子这件事。人脑在处理眼前事物时,并不会将所有脑细胞的记忆都拿出来回忆一遍,我们只会选择跟当前事物相关的部分进行输出,给长时记忆单元加一个“输出门”:$$\hat y_{t}=g_{out}(f(c_t))$$
谁来控制控制门?
从当前设计来看,控制门控制了记忆和决策,但是控制门也应收到其他因素的控制。推导: